
You should see the weights and chart update. To see this in action click on the embedded spreadsheet above and hit F9 to recalculate. It is a particularly powerful method that can be used to find the solution for many non-linear problems. The small Excel Online spreadsheet example embedded below uses the iterative Simulated Annealing method which is a meta heuristic optimisation algorithm to arrive at satisfying weights that are arbitrarily close to the globally optimal weights. How though to make this functionality available online ? Using the Sharpe ratio as the objective function to maximise the optimal portfolio weights can be easily found using the Solver engine’s GRG2 algorithm which can handle such mixed integer quadratic problems with relative ease.
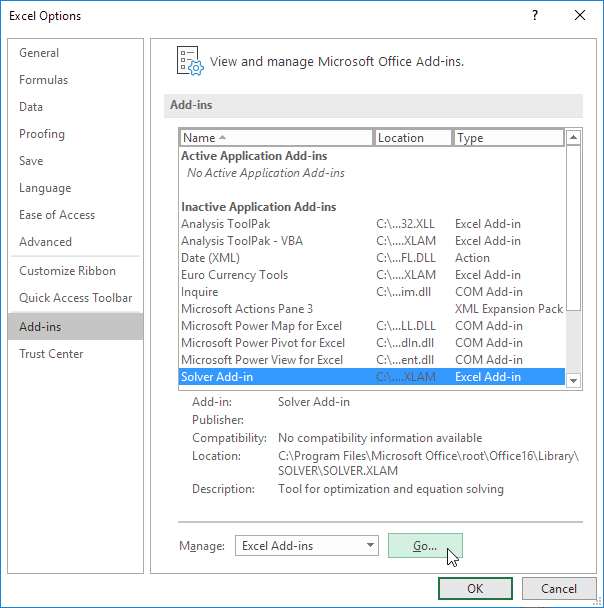
One such example in Finance is the solving of non-linear optimisation problems such as the Mean Variance optimal portfolio problem. Recently Excel have added the ability to use the Solver engine in an online setting but only in edit mode and without the accompanying VBA support it is not possible to automate tasks that would normally be routine in the desktop version of Excel. Note that the discount factor for F to P is just the inverse (1/x) of the factor for P to F.One of the main frustrations of Excel’s online offering is the lack of support for VBA which significantly limits the functionality of web published spreadsheets. The exact discount factor formulas for continuous compounding are given in the table below (where n is the number of years and r is the nominal annual rate). Discount Factors for Continuous CompoundingĬontinuous compounding is not exactly the same as daily compounding. Replace the discount factor symbols (P/G,i%,n), (F/P,i%,n) and (A/P,i%,n) with the appropriate discount factor formula listed in the table. The Excel formulas for (F/G,i%,n) and (A/G,i%,n) are based on the algebraic equivalence of F/G=(P/G)*(F/P) and A/G=(P/G)*(A/P). Nomenclatureĭiscount Rate (effective rate per period) This representation comes from the algebraic equivalence P=F*(P/F). It might help to think of "P/F" as "P given F". The braces around the Excel formula indicate that the formula must be entered as an array function using Ctrl+Shift+Enter.Įxample: To convert F to P, multiply F by the discount factor (P/F,i%,n). The following table lists discount factors used for conversions between common discrete cash flow series, present value, future worth, etc. Discount Factor Table for Discrete Compounding The above formula can be used to calculate an effective annual interest rate for daily compounding by setting p=1 and k to the number of banking days in the year (typically 365 or 360).

To determine the discount rate for monthly periods with semi-annual compounding, set k=2 and p=12. If the compound period is also monthly, the discount rate for a monthly payment period (p=12) simplifies down to i = r / 12. The EFFECT and NOMINAL functions are only used for converting between the effective and nominal annual rates, where p=1. This formula for the effective rate per period is more general than the formula used in the Excel functions EFFECT and NOMINAL. p = number of periods per year corresponding to the basis for n.k = number of compounding periods per year.
To be clear about the nomenclature used in the discount factor table, refer to the following cash flow diagrams for P, F, A, and G.
SOLVER FOR EXCEL 2015 SERIES
Cash Flow DiagramsĪ Cash Flow Diagram can help you visualize a series of receipts (positive values) and disbursements (negative values) at discrete periods in time. With the use of calculators and spreadsheets, the table lookup technique is practically obsolete. In the past, it was common to refer to a discount factor table to look up the number needed to perform a time value of money conversion.

To convert the future value to the equivalent present value, you simply multiple the future value by the discount factor. The discount formula can be written as P=F*(P/F,i%,n), where (P/F,i%,n) is the symbol used to define the discount factor. So, discounting is basically just the inverse of compounding: $P=$F*(1+i) -n. The discounting principle states that if we want to have $F in n years, we need to invest $P right now. The compounding principle states that if we have $P to invest now, the future value will increase to $F=$P*(1+i) n after n years, where i is the effective annual interest rate. Time value of money calculations are based on the principle that funds placed in a secure investment earn interest over time.


 0 kommentar(er)
0 kommentar(er)
